Difference between revisions of "Absorption and Emission"
Cmditradmin (talk | contribs) |
|||
| Line 9: | Line 9: | ||
This article will describe the vibronic progression that can be seen in the absorption and emission spectra. Vibronic progression means that there is a coupling to vibrational modes in your polymer or oligomer as you have an excitation from the ground state to the excited state, or emission from the excited state down to the ground state. | This article will describe the vibronic progression that can be seen in the absorption and emission spectra. Vibronic progression means that there is a coupling to vibrational modes in your polymer or oligomer as you have an excitation from the ground state to the excited state, or emission from the excited state down to the ground state. | ||
[[Image:Transpolyacetylene_vib.png|thumb|300px|]] | |||
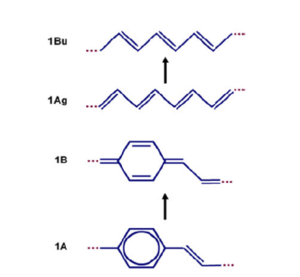
Consider the first optically allowed excited state of the transpolyacetylene which has a 1 Bu symmetry. As the molecule moves from the ground state to that first optically excited state, there is a shift of the double bonds from one bond to the next resulting in a shift of the pi bond densities from one bond to the next. This is described as the reversal of the bond length alternation pattern. If there is a single excitation on a long polyacetylene chain, that modification will be localized somewhere. | Consider the first optically allowed excited state of the transpolyacetylene which has a 1 Bu symmetry. As the molecule moves from the ground state to that first optically excited state, there is a shift of the double bonds from one bond to the next resulting in a shift of the pi bond densities from one bond to the next. This is described as the reversal of the bond length alternation pattern. If there is a single excitation on a long polyacetylene chain, that modification will be localized somewhere. | ||
For PPV, you start with a chain where the rings are aromatic-like, with single, double, single bonds between the rings. The wave functions of the HOMO and the LUMO, and the pi bonding and anti- bonding pattern dictates that as you go to the excited state and an electron leaves the HOMO and goes into the LUMO, you will shift the pi-bond densities in such a way that you end up with a quinoline-like structure. In between the rings, there is a double bond, single bond, double bond, or a larger factor of that kind . | For PPV, you start with a chain where the rings are aromatic-like, with single, double, single bonds between the rings. The wave functions of the HOMO and the LUMO, and the pi bonding and anti- bonding pattern dictates that as you go to the excited state and an electron leaves the HOMO and goes into the LUMO, you will shift the pi-bond densities in such a way that you end up with a quinoline-like structure. In between the rings, there is a double bond, single bond, double bond, or a larger factor of that kind . | ||
[[Image:Transpolyacetylene_vibstretch.png|thumb|300px|]] | |||
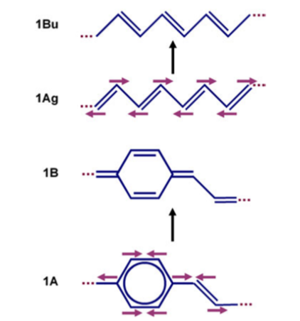
Because of the pi bond densities shifting there will be geometry relaxation when moving from the ground state to the excited state. There will be a coupling with vibrational modes, that leads from the ground state geometry to the excited state geometry. In the case of polyacetylene, these modes brings the top carbon closer to the right, the bottom carbon to the left, then the next top one to the right, bottom one to the left. The same pattern happens for ppv. In other words, there will be strong coupling to vibrational modes that correspond to C-C stretching. Remember the C-C stretching modes in those polymers are at the order of about 1400 - 1600 wave numbers and 0.15 - 0.2 electron volts. | |||
[[Image:C-cbondchange_exitation.png|thumb|300px|]] | |||
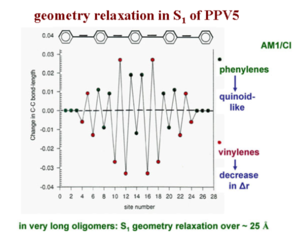
Consider a linear representation of long PPV chain with about 5 rings in order to relate all the bond lengths directly with their modification, from the ground state to the excited state. This plot shows how the C-C bond length changes from the ground state to the S1 excited state in that five ring oligomer. From the plot, it can be inferred that the double bond increases significantly in length by .03 angstrom, where as the single bond actually shortens by about .03 angstrom or more. In other words, the diagram shows the difference in bond length as you go from the optimal geometry in the ground state to the optimal geometry of the S1 state. It is clear that the vinylene double bonds increase in length and the single bonds between rings decrease in length. There is a reversal of the bond length alternation within the vinylene units. Also, within the quinoid rings, you do get an evolution of the bonds that leads you to a more quinoid structure. The geometry relaxation to form the S1 excited state in this oligomer takes place over something like 20 carbons. Polaron relaxation takes place was over about 20 carbons as does the exciton in long chains of PPV. | |||
[[Image:Potentialenergy_surfacechang.png|thumb|300px|]] | |||
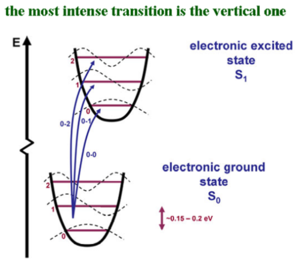
The potential energy surface of the ground state and of the excited state.The potential energy surface of the ground state varies over about 2 electron volts. | |||
The abscissa is the deformation coordinates, which is how the system deforms; the modifications in the coordinates of you system. The lower figure is the optimal geometry of the ground state, and it is different from the optimal geometry of the S1 state that is shown above. The two potential energy surfaces are displaced with respect to one another. The larger the relaxation in the excited state, the larger the geometry of the modification in the excited state, and thus, the larger the displacement would be. If the geometry in the excited state were to be exactly the same as in the ground state, then the two potential energy curves would sit on top of one another. The vibrational levels corresponding to those C-C stretching modes are connected to the geometry relaxation in the excited state and therefore, they are connected to the electronic transition. The dashed curves show the zero vibrational level, the first vibrational level, the 2nd vibrational level and so on. At room temperature, the vibrational mode has energy of on the order of 0.15 to 0.2 electron volts. As you know, room temperature Kt is 0.025. That energy difference between the zeroth vibrational level and the first vibrational excitation is higher than the kinetic energy available at room temperature. In other words, in the ground state, basically all of the oligomers or polymers are in the zeroth vibrational level. | |||
The curve of the dotted lines is the vibrational wave function. In the vibrational ground state, there is no node. In the first excitation state there is one node, and in the 2nd vibrational excited state there are 2 nodes, and so on. The same thing is what you would have if you were to simply look at a particle in the box. In the vibrational ground state, the largest probabilities to find the molecule or the polymer is in the middle. That is the state when the photons strike. The transition takes place faster than the geometry relaxation and thus, there is a vertical transition. Since the potential energy curves are displaced, if you start from the most probable situation in the ground state, and go up, you can have the largest overlap of the vibrational wave functions with the first or the second vibrational level. When there is a coupling of the electronic transition with vibrational modes, the intensity of your electronic transition is modulated by the overlap of the vibrational wave functions as you go up the excited state potential energy surface. | |||
The rule of thumb is that the more the potential energy curve in the excited state is displaced, the larger the relaxation of the geometry in the excited state, and the larger the displacement, the higher the vibrational level, where there will be strong overlap between the ground state vibrational wave function of the electronic ground state and the excited vibrational wave function of the excited electronic state. However, if there were no displacement in the excited state or the two curves were perfectly superimposed on top of one another, then there will be a very strong overlap between the zero vibrational level of the bottom curve and the zero vibrational level of the excited state. But the overlap between the zero vibrational level of the bottom curve and any of the other ones above would be zero. | |||
If the absorption into the first excited state of a pi conjugated system is extremely sharp, there is hardly any geometry relaxation in the excited state because one potential energy curve is right on top of the other. The broadness of the absorption curve indicates a large of the change in geometry in the excited state. For instance, cyanines are important in nonlinear optics. Cyanines and thalocyanines have extremely sharp optical transitions and absorptions. This is because the geometry of the ground state and the excited state are basically identical. However, with systems like oligo PPVs or other conjugated polymers or oligomers, there are geometry relaxations that are significant in the S1 state and the two potential energy surfaces are displaced. The larger the displacement, the higher the most intense transition will be going up the vibrational level scale of the top curve. | |||
Vibronic progressions that go from 0 level below to 0 level above will be referred to as 0-0 absorption. Then you have the 0-1 absorption, 0-2 absorption, 0-3 and so on. For example, 0-2 absorption is the most intense and the geometry relaxations in the excited state will be pretty strong. For 0-1, there is a geometry relaxation but not as large as 0-2. A 0-0 absorption means there is not much geometry relaxation. | |||
In emission first there is absorption and then the excited state comes down to the lowest vibrational level of the lowest excited state during its life time. So the emission will take place from from the 0 level. Then, depending on the overlap of the vibrational wave functions, it will come down to levels ground state levels 2,1 or 0. But in emission, the largest energy transition (or emission) will be the 0-0. Where as in absorption, since you start with the zeroth vibrational level of the ground state, the 0-0 will have the smallest energy of the transmission. | |||
Revision as of 09:24, 3 June 2009
| Previous Topic | Return to Absorption and Emission Menu | Next Topic |
This article will describe the vibronic progression that can be seen in the absorption and emission spectra. Vibronic progression means that there is a coupling to vibrational modes in your polymer or oligomer as you have an excitation from the ground state to the excited state, or emission from the excited state down to the ground state.
Consider the first optically allowed excited state of the transpolyacetylene which has a 1 Bu symmetry. As the molecule moves from the ground state to that first optically excited state, there is a shift of the double bonds from one bond to the next resulting in a shift of the pi bond densities from one bond to the next. This is described as the reversal of the bond length alternation pattern. If there is a single excitation on a long polyacetylene chain, that modification will be localized somewhere. For PPV, you start with a chain where the rings are aromatic-like, with single, double, single bonds between the rings. The wave functions of the HOMO and the LUMO, and the pi bonding and anti- bonding pattern dictates that as you go to the excited state and an electron leaves the HOMO and goes into the LUMO, you will shift the pi-bond densities in such a way that you end up with a quinoline-like structure. In between the rings, there is a double bond, single bond, double bond, or a larger factor of that kind .
Because of the pi bond densities shifting there will be geometry relaxation when moving from the ground state to the excited state. There will be a coupling with vibrational modes, that leads from the ground state geometry to the excited state geometry. In the case of polyacetylene, these modes brings the top carbon closer to the right, the bottom carbon to the left, then the next top one to the right, bottom one to the left. The same pattern happens for ppv. In other words, there will be strong coupling to vibrational modes that correspond to C-C stretching. Remember the C-C stretching modes in those polymers are at the order of about 1400 - 1600 wave numbers and 0.15 - 0.2 electron volts.
Consider a linear representation of long PPV chain with about 5 rings in order to relate all the bond lengths directly with their modification, from the ground state to the excited state. This plot shows how the C-C bond length changes from the ground state to the S1 excited state in that five ring oligomer. From the plot, it can be inferred that the double bond increases significantly in length by .03 angstrom, where as the single bond actually shortens by about .03 angstrom or more. In other words, the diagram shows the difference in bond length as you go from the optimal geometry in the ground state to the optimal geometry of the S1 state. It is clear that the vinylene double bonds increase in length and the single bonds between rings decrease in length. There is a reversal of the bond length alternation within the vinylene units. Also, within the quinoid rings, you do get an evolution of the bonds that leads you to a more quinoid structure. The geometry relaxation to form the S1 excited state in this oligomer takes place over something like 20 carbons. Polaron relaxation takes place was over about 20 carbons as does the exciton in long chains of PPV.
The potential energy surface of the ground state and of the excited state.The potential energy surface of the ground state varies over about 2 electron volts. The abscissa is the deformation coordinates, which is how the system deforms; the modifications in the coordinates of you system. The lower figure is the optimal geometry of the ground state, and it is different from the optimal geometry of the S1 state that is shown above. The two potential energy surfaces are displaced with respect to one another. The larger the relaxation in the excited state, the larger the geometry of the modification in the excited state, and thus, the larger the displacement would be. If the geometry in the excited state were to be exactly the same as in the ground state, then the two potential energy curves would sit on top of one another. The vibrational levels corresponding to those C-C stretching modes are connected to the geometry relaxation in the excited state and therefore, they are connected to the electronic transition. The dashed curves show the zero vibrational level, the first vibrational level, the 2nd vibrational level and so on. At room temperature, the vibrational mode has energy of on the order of 0.15 to 0.2 electron volts. As you know, room temperature Kt is 0.025. That energy difference between the zeroth vibrational level and the first vibrational excitation is higher than the kinetic energy available at room temperature. In other words, in the ground state, basically all of the oligomers or polymers are in the zeroth vibrational level. The curve of the dotted lines is the vibrational wave function. In the vibrational ground state, there is no node. In the first excitation state there is one node, and in the 2nd vibrational excited state there are 2 nodes, and so on. The same thing is what you would have if you were to simply look at a particle in the box. In the vibrational ground state, the largest probabilities to find the molecule or the polymer is in the middle. That is the state when the photons strike. The transition takes place faster than the geometry relaxation and thus, there is a vertical transition. Since the potential energy curves are displaced, if you start from the most probable situation in the ground state, and go up, you can have the largest overlap of the vibrational wave functions with the first or the second vibrational level. When there is a coupling of the electronic transition with vibrational modes, the intensity of your electronic transition is modulated by the overlap of the vibrational wave functions as you go up the excited state potential energy surface.
The rule of thumb is that the more the potential energy curve in the excited state is displaced, the larger the relaxation of the geometry in the excited state, and the larger the displacement, the higher the vibrational level, where there will be strong overlap between the ground state vibrational wave function of the electronic ground state and the excited vibrational wave function of the excited electronic state. However, if there were no displacement in the excited state or the two curves were perfectly superimposed on top of one another, then there will be a very strong overlap between the zero vibrational level of the bottom curve and the zero vibrational level of the excited state. But the overlap between the zero vibrational level of the bottom curve and any of the other ones above would be zero. If the absorption into the first excited state of a pi conjugated system is extremely sharp, there is hardly any geometry relaxation in the excited state because one potential energy curve is right on top of the other. The broadness of the absorption curve indicates a large of the change in geometry in the excited state. For instance, cyanines are important in nonlinear optics. Cyanines and thalocyanines have extremely sharp optical transitions and absorptions. This is because the geometry of the ground state and the excited state are basically identical. However, with systems like oligo PPVs or other conjugated polymers or oligomers, there are geometry relaxations that are significant in the S1 state and the two potential energy surfaces are displaced. The larger the displacement, the higher the most intense transition will be going up the vibrational level scale of the top curve.
Vibronic progressions that go from 0 level below to 0 level above will be referred to as 0-0 absorption. Then you have the 0-1 absorption, 0-2 absorption, 0-3 and so on. For example, 0-2 absorption is the most intense and the geometry relaxations in the excited state will be pretty strong. For 0-1, there is a geometry relaxation but not as large as 0-2. A 0-0 absorption means there is not much geometry relaxation.
In emission first there is absorption and then the excited state comes down to the lowest vibrational level of the lowest excited state during its life time. So the emission will take place from from the 0 level. Then, depending on the overlap of the vibrational wave functions, it will come down to levels ground state levels 2,1 or 0. But in emission, the largest energy transition (or emission) will be the 0-0. Where as in absorption, since you start with the zeroth vibrational level of the ground state, the 0-0 will have the smallest energy of the transmission.
| Previous Topic | Return to Absorption and Emission Menu | Next Topic |